Demonstrating cosmic ray induced electromagnetic cascades
Peter Dunne
Preston College, Preston, Lancashire, UK
Introduction
The Earth is being continuously bombarded by high energy particles from deep space. The particles are mainly high energy protons together with a small component of helium nuclei, heavier nuclei and electrons. The energy range is enormous with some particles having energies of the order 1020 eV.
These primary cosmic rays hit the Earth at a rate of about one particle per square centimetre per second. They collide with atoms in the atmosphere and produce large showers of newly created secondary particles the progeny of which can be detected at ground level. The initial interactions in the upper atmosphere produce large numbers of charged and neutral pions. The charged pions decay into muons and muon neutrinos whereas the uncharged pions decay into pairs of high energy photons which become the starting points of large cascades of electrons, positrons and gamma rays. The resulting flux of particles at ground level consists mainly of these muons and electrons/positrons in the ratio of roughly 75 to 25 percent.
The muons lose their energy gradually by ionisation of the material through which they pass. As they start with high energies they have the capacity to ionise many atoms before their energy is exhausted. Also, as they travel at nearly the speed of light, they tend not to ionise very efficiently and hence can travel through substantial lengths of matter, some metres of lead, before being stopped.
The process is a little different for the electrons. Theory shows that ionisation of the medium is not the predominant energy loss mechanism for relativistic electrons, high energy electrons lose energy more efficiently through the emission of electromagnetic radiation as they are decelerated in the presence of matter. If ionisation had been the main mechanism for slowing the electrons down then they might have had penetrative properties comparable to those of the muons, but the radioactive energy loss mechanism ensures that about 15cm of lead is sufficient to stop them.
The different energy loss mechanisms allow the sea level particle flux to be split into
two main components. The penetrating muon part of the ground level flux is referred to as
the ‘hard’ component and the easily absorbed electron part is called the
‘soft’ component.
Electromagnetic cascades
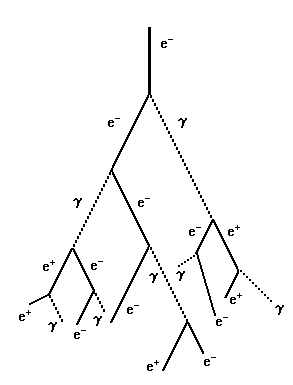
The decay of a neutral pion into a pair of high energy gamma rays is the starting point of an avalanche of electrons, positrons and further gamma rays. This avalanche is known as an electromagnetic cascade. The process starts when one of the gamma rays passes close to the nucleus of an atom. Even though the gamma ray carries no electric charge its electromagnetic nature allows it to interact with the strong electric field of the nucleus to cause the materialization of an electron-positron pair. The energy required for pair creation is about 1 MeV, the gamma rays can have a thousand times that energy and hence the electron-positron pair produced can move on sharing nearly all the energy of the initiating gamma ray. If these fast moving electrons and positrons go on to pass close to other nuclei then they will suffer accelerations due to the positive charge of the protons. An accelerated charged particle will emit electromagnetic radiation. The intense accelerations can produce further gamma rays capable of producing more electron-positron pairs. The cycle of pair-production and gamma ray generation continues with the original gamma ray energy eventually manifesting itself as many particles. The process is shown schematically in figure 1.

Figure 1. Schematic representation of an electron initiated electromagnetic cascade
The cascade generation ceases when the shares of energy get sufficiently small such that the electrons are no longer capable of radiating efficiently; the relatively slow moving electrons are then brought to rest by ordinary ionisation processes. The electron energy at which the main energy loss mechanism changes from radiation losses to ionisation losses is known as the critical energy Ec. The critical energy for electrons in lead is about 7.6 MeV.
Whilst the electromagnetic cascade can grow over a large distance in air it is confined
to much smaller regions in solids where the number of atoms per centimetre path length is
greater. If the material is made up of atoms with a high atomic number then the greater
nuclear charges can produce greater accelerations and so the cascade process can develop
more readily than it would in a material with a lower atomic number.
Electromagnetic cascades in lead
In his 1964 popular account of the historical development of the understanding of the nature of the cosmic radiation (1), Bruno Rossi describes the crucial experiments that led to today’s picture. He recounts how, at the age of 24 in 1930, he built his own Geiger-Mueller counters and developed vacuum tube coincidence electronics to enable him to use groups of GM tubes in an investigation into the cosmic ray penetration of dense materials. He found that a substantial proportion of the cosmic radiation detected at sea level could penetrate over 1m of lead.
About the same time, investigators using cloud chambers reported observations of multiple tracks associated with the apparent generation of secondary particles close to the walls of the chamber. Rossi pursued this by using a coincidence arrangement of three GM tubes in a triangular array within a lead enclosure in order to record the generation of groups of particles. The arrangement is shown in figure 2.
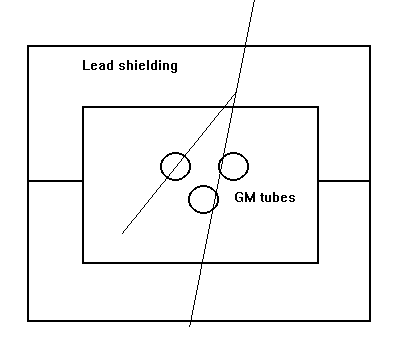
Figure 2. Rossi's apparatus for investigating cosmic ray showers in lead.
A triangular arrangement was used to cut out the possibility of a single particle discharging all the counters at the same time. He was surprised to record a high rate of coincidences, as many as 35 per hour in some cases. When the upper part of the lead shielding was removed the coincidence rate fell to about 2 coincidences per hour. Even this lower coincidence rate was surprising since counter statistics associated with random coincidences predicted a much lower value (see appendix 1). The background coincidence rate can now be understood in terms of showers of particles produced in the air above the counters.
The investigations were developed to see how the coincidence rate varied with thickness of lead placed above the counters. It was found that the rate increased steadily with thickness of lead, reaching a maximum between 1 and 2 cm then falling steadily to about half of the peak value as the lead thickness increased to about 5cm (figure 3).

Figure 3. Shower curve obtained by Rossi using a triangular arrangement of GM tubes
The rapid fall-off of the coincidence rate beyond the peak of the shower curve made it clear that the particles responsible for the production of the groups of particles were not the same as those capable of penetrating 1m of lead with ease.
The explanation of the processes involved in electromagnetic cascades developed in the years that followed. Dirac had already predicted the existence of positrons and Carl Anderson produced cloud chamber evidence of positive electrons. In 1934, Hans Bethe and W. Heitler considered in detail what happened when a charged particle passed through the strong electric field of an atomic nucleus. They found that, at high energies, the particle is likely to release a large fraction of its energy as a photon. The picture of the deceleration induced emission of high energy gamma rays (called bremsstrahlung - or braking radiation) and the subsequent materialization of an electron-positron pair (pair production) began to develop. The theory enabled physicists to calculate the typical numbers of electrons and positrons likely to emerge below a given thickness of lead when a relativistic charged particle or a high energy gamma ray entered it from above. The graphs of the number of shower electrons against lead thickness had characteristics similar to those of the number of coincidences recorded against absorber thickness (figure 4).
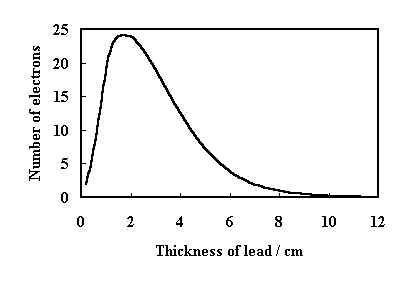
Figure 4. An example of a theoretical prediction of the variation of the number of shower particles beneath a lead absorber as a function of thickness of lead (from Rossi(1))
One can expect the two curves to have similar shapes since the probability of recording a coincidence with the three GM tubes is directly related to the number of electrons appearing below the plates.
The analysis of many sets of experimental data showed that the cascade theory adequately explained the features of the showers.
Reproducing Rossi's cascade experiment
Suitable lead absorbers can be made from lead flashing used in the building industry. It works satisfactorily with standard GM counters connected in a coincidence arrangement through an ordinary AND gate. The coincidence rates are smaller than those reported by Rossi but the shower curve develops well if long timing intervals are used.
Our exploratory investigations gave satisfactory results at the first try.
We obtained twenty-four 20cm x 20cm sheets of lead flashing, each with a thickness of about 1.8mm, from the Construction department of the college. Three MX168 GM tubes were arranged at first in a triangular array and then later in a crossed arrangement (figure 5).
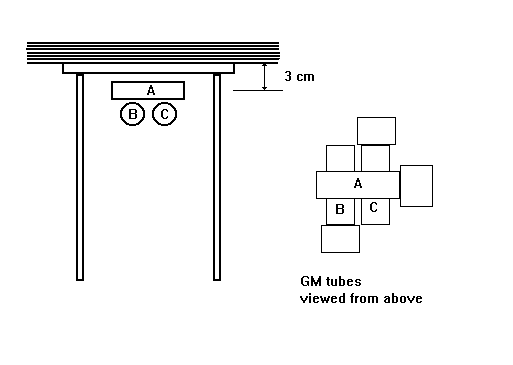
Figure 5. Experimental arrangement for reproduction of the shower curve

The configurations were such that a single particle was unlikely to trigger all three GM tubes at the same time. The size of the GM tube holders dictated the spacing of the tubes in the triangular arrangement, the crossed arrangement allowed the tubes to be placed more closely together and produced a higher coincidence rate. Both arrangements gave a comparable coincidence rate in the absence of shower producing absorbers.
The lead absorbers were supported by a standard laboratory Bunsen burner tripod.
The GM tubes were driven by Unilab GM tube EHT units each having a pulse output of height 4V and a measured width of about 30 m s. The three pulse outputs were connected to a three input AND gate formed using two NAND gates of a 7410 chip. The output of the AND gate then drove a Unilab digital display.
Calculation showed that the expected number of ‘accidentals’, spurious coincidences due to three unrelated GM tube pulses occurring at the same time, would be of the order 5 x 10-7 per hour i.e. the accidental rate would be negligible (see appendix 1).
As the maximum count rate obtained by Rossi occurred between 1cm and 2cm of lead we placed 10 sheets of the flashing on the tripod and obtained a coincidence rate of about 4 per hour. We then removed the ten sheets and ran the arrangement for a full day with no absorbers. We got a count of 8 coincidences in 24 hours without the lead. We accepted that our apparatus was simply not as sensitive as Rossi’s but decided to persevere. We initially decided to count for 24 hours for each reading and increase the lead thickness at a rate of two sheets per day. It soon became clear that whilst the overall count rate was low, our rough and ready experiment produced a shower curve with the same characteristics as those shown in Rossi’s account. We found that placing the GM tubes about 3 cm beneath the lead produced a higher count rate and allowed us to count for 12 hour intervals. A typical graph is shown in figure 6.
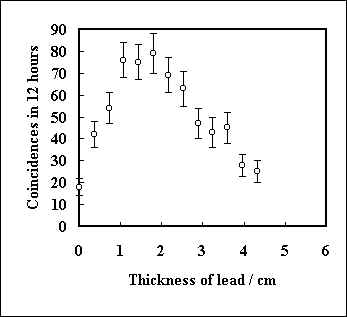
Figure 6. Example of an experimental shower curve obtained using the apparatus shown in figure 5
The peaks of the graphs obtained occurred at about 10 sheets (18 mm) in the same area of the graph as found by Rossi. The simplified theory of the process, described in appendix 2, suggests that the peak of the graph should occur at a thickness tmax given by the equation:
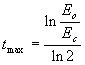
where t is measured in radiation lengths LR, E0 is the energy of the incoming particle and Ec is critical energy for the material below which the electrons tend to lose energy by simple ionisation rather than by bremsstrahlung processes. The equation rearranges to:
![]()
Using the accepted values of LR = 0.56 cm and Ec = 7.6 MeV for electrons in lead, a graph peak at 1.8cm corresponds to 3.21 radiation lengths. The equation above yields a value for the average energy of the incident electrons of the order 70 MeV. This is an impressive value when one considers that the standard radioactive sources used in schools and colleges have energies of no more than a few MeV.
Rossi reported a peak coincidence rate about 4 times as much as ours. We assume that he
might have had a greater collection area and/or GM tubes that were more sensitive to the
radiation. Our MX168 tubes have a sensitive length of about 4cm and a diameter of about
2cm giving an effective collection area of about 8cm2 per tube. In his 1952
book, High Energy Particles (4), Rossi describes typical GM tubes used in early cosmic ray
work with a length of the order 30cm and diameter 2cm giving an effective collection area
about 7 times greater than ours; it is likely that the difference in count rate can be
accounted for by the differences in GM tube size and the sensitivities of the detectors.
Appendix 1 Calculating the rate of ‘accidentals’ in coincidence arrangements
‘Accidental’ coincidences occur when unrelated pulses from the detectors coincide by chance. Simple probability arguments can be used to produce an estimate of the expected coincidence rate.
(1) Two counters
We assume that each counter has output pulses of width dt. The counters are labeled A and B. Let us assume that a pulse arrives at counter A. If counter B produces a pulse within a time interval 2dt following the start of pulse A then a coincidence will be recorded; the situation is illustrated in figure 7.
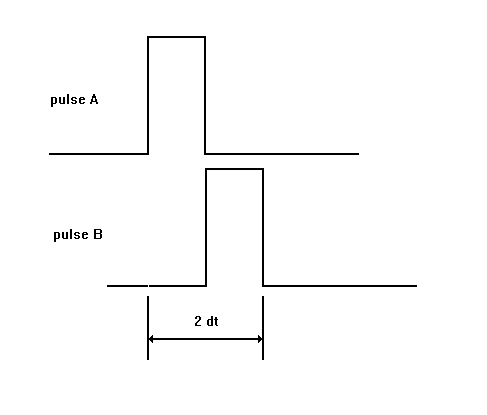
Figure 7. Coincidence interval for two pulses of width dt
If counter A produces nA pulses in one second then then the total time available for B to produce a coincidence will be the fraction 2nAdt of a second. If B produces pulses at a rate nB per second then over a long time interval we can expect the number of accidental coincidences to be:
![]()
(2) Extending the argument to three counters A,B,C
We assume that counter A produces a pulse first. The probability that the pulse from B will coincide with that from A will be given by:
![]()
By an argument similar to that given above, the probability that a pulse from a third counter, C, will occur within a time interval 2dt of the start of pulse A will be given by the expression:
![]()
The probability that both B and C will occur within 2dt of A is then the product of the two probabilities i.e.
![]()
The expected number of accidentals with three counters acting in coincidence will then be:
![]()
However, this turns out to be a bit of an oversimplification: it has ignored situations where two of the counters might be triggered together by a single particle passing through them and then produce a chance coincidence with the third. This kind of situation turns out to alter the numerical multiplying factor from 4 to a higher value but leaves the overall dt2 factor intact. A full mathematical treatment (2) that takes into account the Poisson distribution of interpulse times produces the same equation but with the multiplying factor of 4 replaced by 3.
In the experiment described above, the pulse width dt had a value of 30 m s. The average count rate from each counter was 20 per minute. Using the equation derived above we get an expected accidental rate of:
n(A.B.C) = 4.(20/60)3.(30 x 10-6)2 per second
i.e. =1.3 x 10-10 per second.
This becomes an expectation of about 5 x 10-7 accidentals per hour.
Appendix 2 Electromagnetic cascade theory
The simple model of the electromagnetic cascade presented here is described in detail
in Particle Physics by Martin and Shaw (3) and in High Energy Particles by Rossi (4).
1. Radiation length
It can be shown that, for relativistic electrons, the average rate of energy loss per cm path length due to bremsstrahlung is directly proportional to the particle energy. The relationship is given by the equation:
![]() (1)
(1)
where LR is called the radiation length of the material.
The radiation length for electrons of mass m passing through a material of density na atoms per cm3 and atomic number Z is given by the equation:
(2)
where a (=1/137) is the fine structure constant.
From equation (1) we can see that a particle entering an absorber with an initial energy E0 will have an energy given by:
![]()
after passing through x cm of absorber.
The radiation length can be interpreted as the average thickness of material that reduces the mean energy of the charged particle by a factor e. The value of LR for electrons in lead is 0.56 cm, for iron it is 1.8 cm and for aluminum it is 8.9 cm.
It can be seen from equation (2) that LR is proportional to mass2. As the mass of the muon is some 200 times that of the electron then it can be expected to have a radiation length much greater than that of the electron. This explains why muon energy loss by bremsstrahlung is negligible compared with that of electrons and hence the muons are capable of traversing much greater lengths of absorbing material before being brought to rest.
High energy photon absorption through pair production also turns out to have an exponential character. The rate of attenuation of a collimated beam of I photons per second is described by the equations:
![]()
![]()
where l is the mean free path for the photons in the absorber.
The mean free path for photon absorption through pair production is related to the radiation length for electron bremsstrahlung by the equation:
![]()
It can be seen that the two characteristic lengths are comparable in magnitude.
The general features of the electromagnetic cascade can be accounted for by a
simplified model of the successive generation of photons and electron-positron pairs.
2. The simplified cascade model
The model is based upon the following restrictions:
(i) the incoming charged particles have a starting energy E0 that is much greater than the critical energy, Ec, below which ionisation losses predominate over pair production i.e. E0 >> Ec ;
(ii) we assume that each electron with E0 > Ec travels one radiation length and then gives up half of its energy to a bremsstrahlung photon;
(iii) we assume that each photon produced with energy Eg > Ec travels one radiation length and then creates an electron-positron pair with each particle carrying away half the energy of the original photon;
(iv) electrons with E < Ec cease to radiate and then lose the rest of their energy by collisions.
The process is illustrated in figure 8.
Figure 8. The simplified electromagnetic cascade model. Values of t represent successive radiation lengths.
This simple branching model suggests that after t radiation lengths the shower will contain 2t particles. There will be roughly equal numbers electrons, positrons and photons each with an average energy given by:
![]()
The cascading process will stop abruptly when E(t) = Ec .
The thickness of absorber at which the cascade ceases, tmax, can be written in terms of the initial and critical energies i.e.
![]()
hence
![]()
and

The model suggests that the maximum shower depth varies as the logarithm of the primary
energy, a feature that emerges from more sophisticated models of the process and is
observed experimentally. It also predicts that the shower curve should rise rapidly to a
peak value and then fall to zero. The broad peak of the experimental curve can be
interpreted in terms of a spread of energies of the incoming particles. Experiment also
shows that the curve does not eventually drop to zero but instead has a long tail. The
long tail can be interpreted as being due to muon interactions producing knock-on
electrons capable of making a contribution to the cascade process.
References
[1] Rossi B 1964, Cosmic Rays (London: George Allen and Unwin)
[2] Schiff L I, Statistical Analysis of Counter Data Phys Rev, 50, 88 (1936)
[3] Martin B R, Shaw G, 1992 Particle Physics (Chichester: John Wiley and Sons)
[4] Rossi B 1952, High Energy Particles (Eaglewood Cliffs N J:Prentice-Hall Inc)