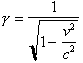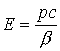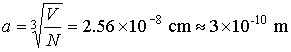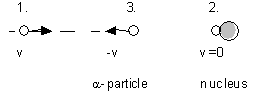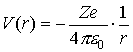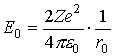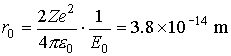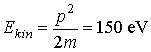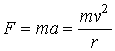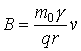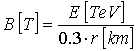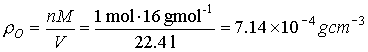Exercises on
High Energy Physics
by Dieter.Bartneck@sz-online.de
Constants and Formula used in High Energy Physics
Exercise 1 - Atoms
Exercise 2 - Nuclei
Exercise 3 - Particle Waves and Relativity
Exercise 4 - Virtual Particles
Exercise 5 - Accelerators
Exercise 6 – Particle Beam
Constants and Formula used in High Energy Physics
|
Avogadro
constant
|
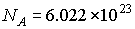
|
|
Boltzmann
constant
|
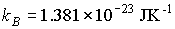
|
|
speed
of light (in vacuum)
|
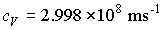
|
|
electric
field constant
|
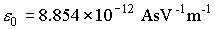
|
|
magnetic
field constant
|
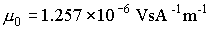
|
|
elementary
charge
|
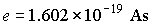
|
|
rest
mass of electron
|
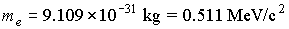
|
|
rest
mass of neutron
|
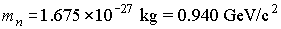
|
|
rest
mass of proton
|
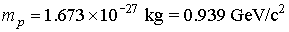
|
|
atomic
mass unit
|
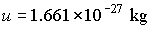
|
|
Planck’s
constant
|
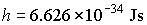
|
|
|
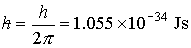
|
contents
|
energy
and momentum
|
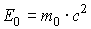
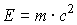
|
|
|
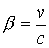
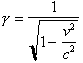
|
|
|
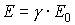
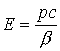
|
|
|

|
|
energy
frequency relation
|
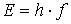
|
|
Heisenberg
uncertainty relation
|
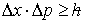
|
|
|
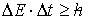
|
|
de
Broglie wavelength
|
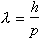
|
|
Lorentz
force
|
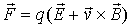
|
contents
Try to estimate the
radius of one gold atom!
Hints
1.
Take a cube with sides of one centimetre. Divide the cube into smaller
cubes, one for each gold atom.
2.
You’ll need Avogadro’s constant, the density of gold and the mass of
one gold atom.
Solution
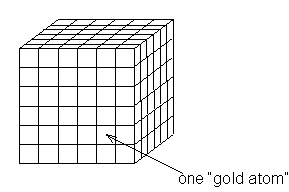
atomic weight and density of gold:
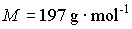
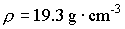
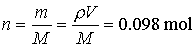

There are 6.1022
atoms in the cube.
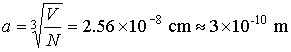
One atom of gold has a diameter of 3.10-10
m, which gives about 10-10 m for the radius of an atom.
contents
Try to estimate the
radius of the nucleus of a gold atom!
Hints
1.
Rutherford observed in his famous scattering experiments with 6 MeV a-particles,
that some of the particles were very strongly deflected, although very few were
flying back to the direction of the source.
2.
The experiment shows that the nucleus has a very strong electric field
concentrated almost in one point. The repulsive Coulomb potential the a-particles
feel, stops them if they are moving in the direction of the centre of mass, at a
certain distance from the nucleus.
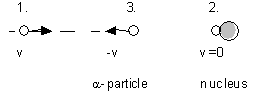
3.
Assume that the a-particles
stop when all their kinetic energy has been converted into electrostatic
potential energy.
Solution
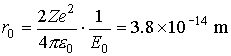
The radius of the nucleus of gold
should be in the order of 10-14 m.
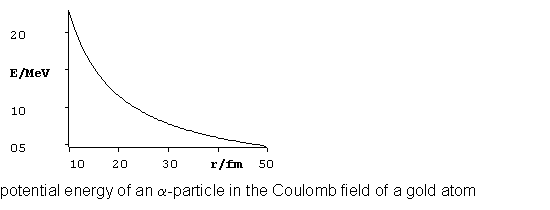
N.B. This calculation assumes that the
gold nuclei do not recoil from the a-particles.
This is a good approximation as the mass of a gold nuclei is much larger than
that of an a-particle.
contents
What energy particles
(e.g. electrons) are needed to investigate the inner structure of
·
atoms,
·
protons and neutrons?
Hints
1.
As in a microscope, the resolution is determined by the wavelength.
2.
At higher energies, particles become relativistic.
Solution
·
To investigate the crystal structure of a
material you will need a resolution of about 1.10-10 m.
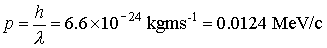
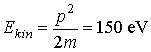
Electrons are non-relativistic at this energy because it is much less than their
rest energy of 0.5 MeV.
·
The dimension of the nucleons is smaller than 1.10-15
m.
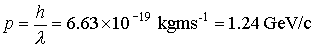
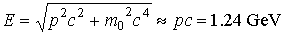
Electrons are relativistic at this energy. You don’t have to consider their
rest mass.
contents
Knowing the dimension of
neutrons and protons, you can estimate the mass of the particle, which is
responsible for the interaction between the nucleons.
Hints
1.
The interaction between charged particles is carried by photons. Because
the range of this interaction is infinite, the rest mass of a photon has to be
zero. The interaction between nucleons is limited to a range of about 10-15
m.
2.
The Heisenberg uncertainty relation allows fluctuations of energy for a
very short time, so "virtual" particles can be created, which are
responsible for the interaction between particles.
Solution
The uncertainty relation for a distance from 10-15
m allows a maximum energy deviation of about 200 MeV. A particle which is
responsible for the interaction of two nucleons should have a mass in the
order of 200 MeV but can only
exist for about 10-24 s. According to the prediction of Yukawa
(Nobel prize in 1949) Powell and collaborators found the p-meson
in 1947 with a mass of about 140 MeV.

contents
What dimensions (radius,
magnetic field, revolution frequency) should an accelerator have to produce Z
and W bosons, which are responsible for the weak interaction between particles?
Is it possible to build an accelerator that replicates the maximum energies of
cosmic ray on Earth?
Hints
1.
The Large Electron Positron Collider (LEP) a storage ring at CERN, has a
length of about 27 kilometres. The electrons and positrons are moving at
ultra-relativistic speed.
2.
The mass of the Z boson produced in LEP1 (to 1995) is about 91 GeV. The
mass of the W boson is about 80 GeV; the LEP2 (to 2000) runs at an energy
sufficient to produce W's in pairs. Using a collider you have twice the energy
of the beam to create new particles.
3.
The highest energy of cosmic ray ever recorded is over 20 TeV.
Solution
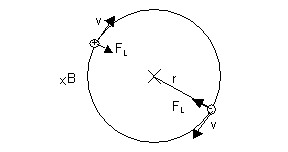
For the calculation of the magnetic
field for relativistic particles one can use:
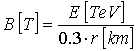
LEP: reff
= 3 km Only 2/3
of the 27 km are used for bending magnets.
B = 0.1 T for Z's and B = 0.18 T for W's in pairs, frev = 11
kHz
To get the
energy of 20 TeV at a magnetic field of 10 T (maximum with superconducting
magnets) you have to build a tunnel, which has twice the radius of the LEP.
N.B. The
reason for the big radius of the LEP tunnel is the synchrotron radiation of
the accelerated electrons and positrons, which energy is proportional to g3/r.
contents
Compare the density of
gold and oxygen to the density of a particle beam in an accelerator.
Hints
The
particle beam is divided in so-called bunches in an accelerator flying around
like cigars at a certain distance. One bunch for the Large Hadron Collider (LHC)
at CERN has a length of about 15 cm and a radius of about 17 mm,
filled with 1011 protons.
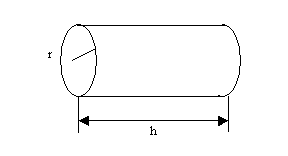
Solution
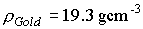
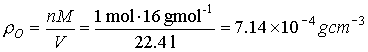

The
density of the beam bunch is between the density of a solid and a gas.
contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()