Exercises on High Energy Physics

                                                by   Harri.Hakulinen@jnor.joensuu.fi

Contents

Particle accelerators

Exercise 1	Exercise 8
Exercise 2	Exercise 9
Exercise 3	Exercise 10	Background
Exercise 4	Exercise 11
Exercise 5	Exercise 12
Exercise 6	Exercise 13
Exercise 7	Exercise 14

The Standard Model

Exercise 15

 

 

Particle accelerators

Exercise 1

The plan for the LHC is to use the LEP’s tunnel  to produce protons of very high energy.

Solution

a) What is the maximum energy for a tunnel 27 km long with a maximum magnetic field in the vacuum tube of 8.36 T.

According to Newton II  F = ma and when the beam is a ring we get

and the momentum of the beam particle is p = mv  where m is the total mass on the particle.  So we get

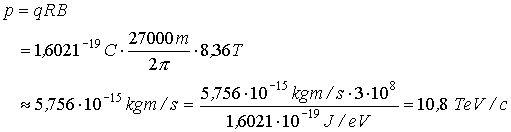
The effective length of the ring is less than 27 km, because the maximum energy is planned to be 7 TeV.

If  the energy of protons is 7 TeV,  the momentum of protons, according to Einstein, is given by

           and so

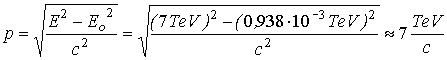
or

  The bending of the effective length of the LHC-ring is then

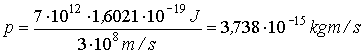
There are components other than the bending magnets in the ring, for instance, accelerating cavities and focusing magnets.

The percentage of the straight part in the accelerator is

Contents

E xercise 2

In the LHC ring there are 2835 bunches in each ring which will collide which each other once in each detector. How many collisions of bunches are there in

a)     one second,

b)    one run which will last about 10 hours.

Solution

The bunches travel at nearly the speed of light  so they meet every

so the frequency of collisions is

It should be 40 MHz, but there are some holes in the beam in other words some bunches are missing. This is the reason for the pacman effect, that will be eating the beam little by little, because those bunches that are not colliding will behave in a strange way and somehow eat the other bunches or make more holes to the beam.

And in 10 hours there will be about

          .

The data that will be collected from the collisions will about the amount of 10000 Britannica Encyclopedia per one second.

Contents

Exercise 3

The time interval between bunches arriving at one the detector is 25 ns. How many collisions occur in one second and what is the rate at which the bunches meet in the accelerator?

Solution

There are

The event rate that the bunches meet is then 40 MHz.

Contents

Exercise 4

The current of the proton particle beam in LHC  is 0.5 A. How many particles are there in one bunch if there are 2835 bunches in a ring  and the time interval between the bunches is 25 ns?

Solution

The current is

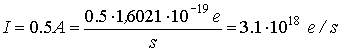
The time is 25 ns so we get

          .

 Contents

Exercise 5

What is the total energy which is stored in the protons in one ring, when the protons have the maximum energy 7 TeV and there are 10¹¹ particles in one bunch?

Solution

The total energy in the beam is

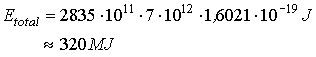
If you compare this to for instance to a boat which is traveling at the speed 3 m/s which 11km/h, the mass of the “boat” should be

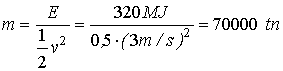
So quite a big boat.

 Contents

Exercise 6

What is the current if there are  10¹¹particles in one bunch?

Solution

The current is

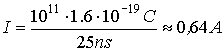            or

          .

 Contents

Exercise 7

How many turns can a proton beam stay vertically in the tube if you do not focus it?

Solution

The diameter of the vacuum tube in LHC is 18 mm. From the kinematic equations we get

            and  the time is

          .

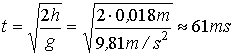In this time the proton will go

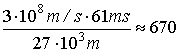            turns. 

The beam should last 10 hours and therefore

           turns.

This is why the accelerator must have some focusing components.

 
Contents

Exercise 8

For how long would Mika Hakkinen have to drive around the ring at a constant 320 km/h if he is to travel as far as a proton in LHC travels in one second.

Solution

It will take

   = 937,5 h = 39 days ( and nights).

 Contents

Exercise 9

In the LHC accelerator at CERN, the  increase in current in the superconducting magnets can be  10 A per second. How long will it take to reach the maximum current of 11700 A?

Solution

The time is

          .

 Contents

Exercise 10

The basic element of the LHC is 15 m long and made of steel. How does the length of the tube change when the tube is cooled to 1,9 K compared to the room temperature 20^oC?

No solution
Particle reactions

 Contents

Background

The event rate gives you information on how many events occur in head-on collisions in the particle detector and is defined as

where  f_rev  is the how many times one bunches will go around the ring, N₁ and N₂ are the numbers of particles in each bunch going in revert direction. A is the cross-sectional area of the beam and s is the cross section of a certain event (some sort of probability for a certain event to happen). The first part is called the luminosity L and is defined as

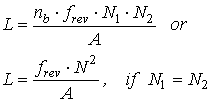
So the event rate can be expressed as

          .

If you know the frequency the bunches meet  f_bunch  the event rate is

Contents

Exercise 11

The luminosity of LEP was 100 × 10³⁰  cm^-2s^-1. If the cross section of a certain event is 1.0 × 10^-24 cm²  or one barn (b). How many  events will occur in one second ?

Solution

The event rate in LEP when the cross section is 1 barn is

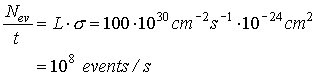
The time for one revolution is

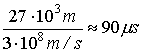
and the frequency for revolution is

          .  

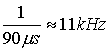There are four bunches in a ring so the frequency between collisions is

and the time interval between collisions is

          .

  Contents

Exercise 12

The luminosity of LHC is in the beginning 1 × 10³³  cm^-2s^-1. The estimated cross section to create a Higgs boson to produce two g is 50 fb. How many  events do you wait to see in one second ?

Solution

The event rate is

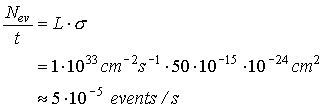
You should wait

until one Higgs boson should appear.

In Tevatron-accelerator  in Chigago the luminosity in the new machine is about 10³⁰ cm^-2s^-1 . How long should you wait for Higgs in process where Higgs decays to two photons if the cross section is the same. Tevatron has the maximum energy of only 1 TeV and cross section depends on the energy so it is not quite true.

The event rate is

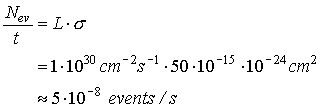
You should wait

            for the first Higgs and

for 10 Higgs bosons  to make sure that it really is a Higgs boson.

They start the experiment these days and the LHC will finished in 2006. So the race to find Higgs will be tight.

If the cross section for Higgs boson to produce top and antitop is 20 pb, so you would expect

and you should wait only 50 seconds.

  Contents

Exercise 13

The luminosity of the LHC is   1 × 10³⁴  cm^-2s^-1. If there are 17000 events in 100 ms, what is the cross section in barns of this event ?

Solution

The event rate is

so the cross section of the event is

  Contents

Exercise 14

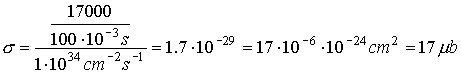
The cross section of a reaction to produce the Z-particle, one of the weak interaction carriers, in LEP where the collision happened between electrons and positrons, is 32 nbarn at the beam energy 91 GeV. How long did they have to wait for the first event if the luminosity was 23×10³⁰cm^-2s^-1?

Solution

The event rate is

.

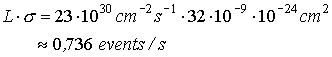So time was approximately 1/(0,736 1/s)  = 1,4 s  when the first Z-particle was made out of energy. 

  Contents

The Standard Model

Background

There are three kinds of particles which are made of quarks. The mesons which are made of a quark and an antiquark (qq), baryons which are made of three quarks (qqq) and antibaryons which are made of three antiquarks (qqq).  Only particles made of these combinations have been found.

The theorists assign a color to each quark (red, blue or green) and their anticolor to the antiquarks to explain the above combinations of quarks. The rule is that all particles are white and a particle is white when the quarks inside the particle have 3 different colors or one color and its anticolor.

Another rule is that nobody has seen a particle which does not have an integer charge. The charge must be –1, 0, +1 or +2 because the quark’s charge is either +2/3  or –1/3. For instance three times +2/3 is +2  or  (+2/3) + (-1/3) + (-1/3) is zero or three times –1/3 is –1.

 Contents

Exercise 15

In the standard model how many ground state (spin = 0) mesons and baryons could there exist  if  we had 

a)  4 quarks (u, d, s and c)   or   

b)  6 quarks                    (see the table below).

Hint

When you calculate the charge of the particles in part b)  it could be useful to organize the quarks on the following way:

Solution - Mesons

First we deal with quark and antiquark (q,aq) so mesons.  

Charge can be either zero, plus one or minus one.

Each quark can be with two antiquarks to produce no charge so there are

4 × 2 = 8 possibilities. When the charge is +1 or –1 there are two possibilities for each quark so 8 and so 16 different mesons altogether with 4 quarks.

You can do in the same way, when you have six quarks.

You can combine each quark with three others to get zero charge when there are six quarks so there could be 6 × 3 = 18 different particles.

The final charge is –1 or +1 there are also three possible antiquarks for each quark and so there are 6 × 3 = 18 different possibilities. So there are 36 different mesons when you have 6 quarks in use.

There is also another way. We put all quarks in a table as below.

In this way we  6 × 6 = 36 different mesons on ground state (spin = 0).

  Contents

Solution - Baryons

First we look at the three quark (qqq) - combinations.

First the baryons which have no charge (Q = 0). Every quark with charge +2/3 can connect to another with charge –1/3  in six ways. For instance quark  u to dd, ds, ss, st, tt, dt so 6 ways to do it. And the other c and b also, which have a charge +2/3.  We have 18 different particles.

Next the baryons with charge –1. The quarks from the lower part of the table will connect to each other in 3×3×3 ways and we get 27 different particles.

The same when the charge is  +2 (the upper part of the table). They can connect to each other on 3×3×3 = 27 different ways and we get 27 particles more.

Last is the charge +1 and it is similar to when the charge is zero. You take one particle from the lower part of the table (Q = -1/3) and connect it to two particles from the upper part (Q = +2/3)

Altogether there will be   18 + 27 + 27 + 18 = 90 different particles called baryons.  There are also antiparticles so get 90 particles more and the total number of different baryons is 180. This the case when the baryons are in their ground state where they have the minimum energy. The mixed states and the exited states of quarks are also individual particles and are not included in here.

 Contents