The simplest particle accelerator is a battery. There is a potential difference, V, between its terminals which produces an electric field equal to the potential gradient. A charged particle in this field will feel a force and be accelerated. In electric wires, the electrons undergo too many collisions with the wire’s atomic lattice to gain any speed and the energy is transferred to the conductor as heat, but if the particles are in a vacuum they will accelerate unhindered. The kinetic energy gained by the particle will be equal to the electrical energy lost by the battery:

The standard energy unit of particle physics is derived from this equation: an electron-volt, eV, is the energy gained by a particle with a charge equal to that of the electron (e = 1.6x10^-19 C) accelerated through a potential difference of one volt: 1 eV = 1.6 x 10^-19 J.

Batteries can be put in series to increase the potential difference, but early direct voltage machines were Van der Graff generators. These are still used today, particularly in the initial stages of modern accelerators and are ultimately capable of potential differences of around 10 MV.

In the early 1930’s, Brasch and Lange worked to use the huge potential differences available in lightning storms for accelerating particles. An insulated wire was hung across a valley in the Swiss Alps, with a conducting terminal suspended from it. Sparks several hundred feet long were seen between this terminal and an earthed one on the valley floor but the project was abandoned when Lange was fatally electrocuted.

In 1932 Cockcroft and Walton produced the first nuclear reaction using artificially accelerated particles, bombarding and disintegrating lithium nuclei with protons accelerated to several hundred keV:

Why were their 600 keV protons more effective than 7 MeV alpha particles? Nuclear reactions occur because of the strong interaction which acts between the nucleons in the beam particle and target nuclei. The strong interaction has a very short range and the 600 keV protons get closer to the lithium nuclei than the 7 MeV alpha particles get to the gold nuclei.

The point of closest approach can be calculated by assuming that, at this point, the beam particle has converted all of its kinetic energy into electrostatic potential energy.

Alpha particles: Z = 2

Protons: Z = 1

Lithium: Z = 3

Gold: Z = 79

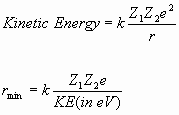
For 7 MeV alpha particles on gold compared to for 600 keV protons on lithium.

These calculations assume that the target nucleus does not recoil: for alpha particles on gold this is reasonable, less so for protons on lithium and probably not at all for alpha particles on lithium. The target nuclei are not floating free in space but are part of the solid lattice, which would complicate a detailed calculation further.

Even so, this is a serious over-simplification. The energy available per beam particle nucleon is an important factor as is the relative size of the alpha particle to the target. Against a small target, the alpha particle is more likely to interact as an alpha particle; with larger nuclei it behaves more as 2 protons and 2 neutrons. This is, in part, due to the very short range nature of the strong interaction in nuclei were nucleons tend to interact only with their neighbours.

Cockcroft and Walton used an a.c. supply to charge several capacitors to a high voltage. These were then discharged so that the potential differences added together. This is called a cascade machine.

Introduction        Direct voltage and cascade machines           Cyclotrons

Betatrons                    Linear accelerators and the synchrocyclotron                Synchrotrons       

    Fixed target verses collider machines        Lepton verses Hadron machines        The Future?