Theoretical Basis for Special Relativity

Basic Formulae

          Einstein’s Special Theory of Relativity describes the motion of particles moving at close to the speed of light. The Newton’s laws of motion are contained within the relativistic equations and provide a good approximate form, valid when v is much less than the speed of light c.

Many high-energy physics experiments have tested Einstein’s theory and show that it fits all results to date.

Einstein’s theory of special relativity is based on two postulates:

1.      The speed of light is the same for all observers, no matter what their relative speeds.

2.      The laws of physics are the same in any inertial frame of reference.

Relativistic Definitions

     In Particle Physics, we are almost always dealing with relativistic particles having the ratio b=v/c comparable to 1.

            The measurable effects of relativity are based on gamma factor :

               (1)

where c is the speed of light and v is the speed of the particle.

The mass of a particle sitting at rest in a frame of reference is m₀.

The mass of the moving particle is :

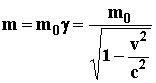
(2)

The total energy of a particle, first derived by Einstein is:

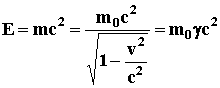                    (3)

The moment is :

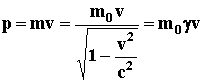               (4)

The relativistic expression for the energy of a particle of mass m₀ and momentum p is:

           (5)

The total energy for a freely moving particle is:

         (6)

where  is the rest energy and T is the kinetic energy. This expression shows that energy and mass are interchangeable. In any particle decay process, some of the initial energy becomes kinetic energy of the products.

            Some quantities, such as the rest mass m₀ , or the speed of light in vacuum are invariant, they do not change with speed.

Others, such as the particle’s coordinates, velocity, energy, momentum, acceleration, etc., depend on the particle motion according to the observer’s frame of reference.

content