Lorentz Transformations

They allow us to derive the relation between different physical quantities in the various inertial frames.

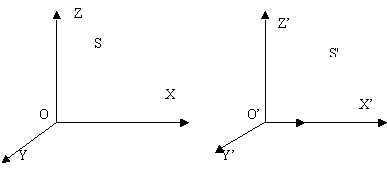
Let’s take two frames of reference S and S’ moving uniformly and rectilinearly with velocity v in the x direction relative to one another.

Lorentz’s transformations enable us to calculate the coordinates of a world point in S’ from those in S and vice versa.

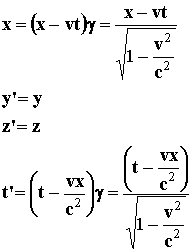               (7)

According to the principle of relativity, both systems are equivalent.

One can obtain x, y, z, t, when x’, y’, z’, t’, are known, using the formulae (7), except that v becomes changed into –v.

            Using these formulae, one can get the length contraction and time dilatation expressions:

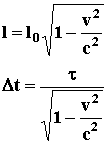       (8)

            Each observer from S and S’ will see a meter stick of the other as shorter than their own, by the same factor g.

            Each observer will measure the duration of an event larger than his own, by a factor g.

            Particle processes are characterized by their own half-life. The half-life of a moving particle appears, to the static observer, to be multiplied by g.

            Let’s study particle decay in flight. In the frame of reference where it is at rest, its lifetime is t (i. e. the proper time).

            An observer in the laboratory frame will see: t=gt . The mean free path in the SL frame is: l=vt=bgct.

            The measured distribution of distances is used to find the particles’ lifetime.

content