Polar light: A nice way to show, how LORENTZ-force works

This experiment can be used as a small experiment only for to show the LORENTZ force or to exercise some useful calculations after showing the experiment.

The idea:

For to understand how particles from the sun -for example electrons- come into our atmosphere and why it happens only –not quite “only”- on the magnetic poles, we will need an electron beam with variable angle to a magnetic field.

Most of us will have a pair of HELMHOLTZ coils. We also need any tube with a free flying visible electron beam. I usually take a model of a BRAUN-tube. To use the tube from the e/m-experiment may be possible.

What can be shown:

1. Place the electron beam parallel to the magnetic field. Nothing happens.

Nice to see. There is a magnetic field and no force to the beam. Teachers may tell their students that there is no force, but they may believe if they can see it.

Problem: The field is not perfect “homogen”, only “nearly nothing” happens. The difference is good to see when compared with step 2.

2. Place the beam in a 90° angle to the field.

Everybody knows what happens … (e/m)

3. Place the beam between 0° and 90°!

The electrons will take their way spiraling (This word I learned from Gron.
Thank You.) “around the magnetic field strings”.

Try some different voltage for the beam and different current for the magnetic field to get a good picture.

If it is tested before the lesson, it will be easy to change something while showing the experiment.

4. Try to find a place at the outer edge of the coils where the field is not homogen.

It is possible to see the electrons spiraling and curving into the coil.

That is what happens near the magnetic poles of the earth!!

Calculations:

(I will do all calculations without vectors.)

to 1. a=0 => F=0, very simple

to 2.

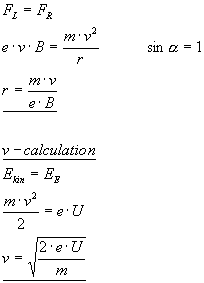
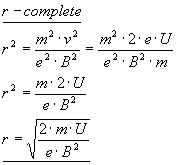
It can be a little exercise to show that the electron is “not relativistic”.

If accelerated with 300 V, the velocity will be

, this is not relativistic.

to 3.

Nice exercise to take apart vectors in orthogonal components.

Some interesting things will happen.

I want to calculate the radius of the spiral and the way between two turns.

Definitions:

Radius:

Only the orthogonal component works for the radius.

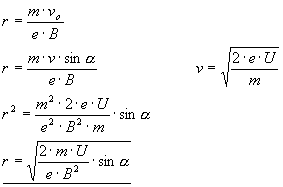
Length:

The parallel component makes the length.

The orthogonal component is needed for the time for one turn.

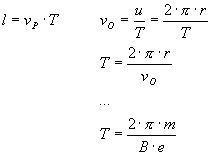
The angle and the voltage have no influence to T.

What about U = 0 or a = 0? Think about it!

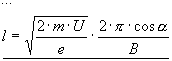
Now everything is clear.