
Electron-positron
Annihilation and Pair Creation.
Compton
Scattering
Fig.1 This bubble chamber picture shows some electromagnetic events such as pair creation or materialization of high energy photon into an electron-positron pair (green tracks), the Compton effect (red tracks), the emission of electromagnetic radiation by accelerating charges (violet tracks) (bremsstrahlung) and the knock-on electrons or delta ray (blue tracks)
Electron-positron Annihilation
The processes of electro-positron annihilation into photons pairs and of pair creation by photon are of interest both theoretically and experimentally.
The electronís antiparticle, the positron, is identical in mass but has a positive charge. If an electron and positron collide, they will annihilate with the production of two gamma photons:
![]()
Fig. 2 Part of a bubble-chamber picture from a neutrino experiment performed at the Fermilab (found at the University of Birmingham). A positron in flight annihilate with an electron. The photon that is produced materializes at a certain distance, along the line of flight, resulting a new electron-positron pair (marked with green)
In the frame of reference related to the electron, the conservation laws are:
![]() (2.1)
(2.1)
where
![]()
the momentum conservation is:
![]() (2.2)
(2.2)
The energy transferred to
![]() is maximum when
is maximum when
![]() is emitted in the direction of the
incident
is emitted in the direction of the
incident
![]() .
.
Hence:
![]() (2.3)
(2.3)
and
![]() (2.4)
(2.4)
but
![]() and
and
![]() because of the zero-masses of
photons.
because of the zero-masses of
photons.
Multiplying (2.4) by c, gives:
![]() (2.5)
(2.5)
Subtracting
![]() from (2.5) and replacing it in (2.3) gives:
from (2.5) and replacing it in (2.3) gives:
![]() (2.6)
(2.6)
Therefore:
![]() (2.7)
(2.7)
where one can calculate the total energy
![]() and momentum of the incident
and momentum of the incident
![]() by using its kinetic energy T:
by using its kinetic energy T:
![]() (2.8)
(2.8)
and
![]() (2.9)
(2.9)
Electron-Positron
Pair Production
When a photon has quantum energy
![]() higher than the rest energy of an
electron plus a positron, one of the ways such as a photon interacts with matter
is by producing an electron-positron pair in the field of nucleus.
higher than the rest energy of an
electron plus a positron, one of the ways such as a photon interacts with matter
is by producing an electron-positron pair in the field of nucleus.
![]()
This process cannot take place in free space because of the conservation laws violation.

Fig.3 Part of a bubble chamber picture (Fermilab'15 foot Bubble Chamber', found at the University of Birmingham). The curly line which turns to the left is an electron. Positron looks similar but turn to the right The magnetic field is perpendicular to the picture plan
The rest energy of the electron is
![]() , so for photons with energies much bigger than
, so for photons with energies much bigger than
![]() , pair production is possible and can be a mode for the interaction of X-rays,
or gamma-rays with matter.
, pair production is possible and can be a mode for the interaction of X-rays,
or gamma-rays with matter.
Compton
Scattering

Fig.3 Part of a bubble chamber picture (Fermilab'15 foot Bubble Chamber', found at the University of Birmingham). An electron was knocked out of an atom by a high energy photon.
Compton scattering is related by crossing symmetry to pair annihilation:
![]() Compton scattering
Compton scattering
![]() Pair annihilation
Pair annihilation
It can be seen that the electron on the left side of the Compton process can be replaced by its antiparticle, the positron, on the other side of the interaction resulting pair annihilation.
Crossing symmetry applies to all known particles, including the photon, which is its own antiparticle.
Generally, in the case of
![]() processes, the crossing symmetry
relates the following interactions:
processes, the crossing symmetry
relates the following interactions:
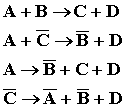
The over bar indicates the antiparticle.
In the Compton effect one can observe a shift in wavelength upon scattering of light from stationary electron. The Compton effect, discovered by Compton in 1923, provided the final confirmation of the validity of Planckís quantum hypothesis that electromagnetic radiation came in discrete mass less packets (photons) with energy proportional to frequency.
Let a photon of frequency
![]() or wavelength
or wavelength
![]() scatter off an electron
scatter off an electron
![]() at an angle
at an angle
![]() like in Fig.1. In collision, it
transfers some energy to the electron
like in Fig.1. In collision, it
transfers some energy to the electron
![]() and emerges at a shift frequency
and emerges at a shift frequency
![]() or wavelength
or wavelength
![]() as
as
![]() .
.
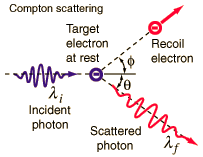
Fig.1 Compton effect
Conservation laws give:
![]() (2.1)
(2.1)
![]() or
or
![]() (2.2)
(2.2)
where
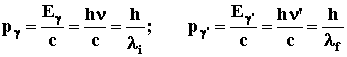 (2.3)
(2.3)
and
![]() (2.4)
(2.4)
Plugging (2.3) and (2.4) into (2.1) and (2.2), one can derive the Compton scattering equation:
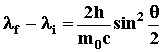
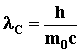 is known as the Compton wavelength.
is known as the Compton wavelength.