Energy-Momentum 4-Vector
![]() The
invariance of "length" of this 4-Vector is associated with the fact that the rest mass of a
particle is invariant under coordinate transformation.
The
invariance of "length" of this 4-Vector is associated with the fact that the rest mass of a
particle is invariant under coordinate transformation.
This ca be defined through the velocity 4-Vector:
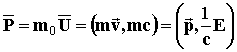 or
or
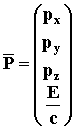 (21)
(21)
where m0 is the
particle rest mass and
![]() .
.
The length of the energy-momentum 4-Vector is given by:
![]() (22)
(22)
and represents the rest energy of the particle. The invariance is associated with the fact that the rest mass is the same in any inertial frame. This relation is also true for mass-less particles, such as the photons, for which E=pc or p=E/c. These ones are related to a frequency n and wavelength l:
![]() and
and
![]()
The Lorentz transformation can be expressed in matrix form:
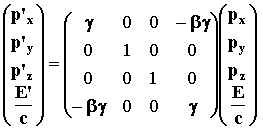 (23)
(23)
Thus:
 (24)
(24)