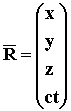 (9)
(9)Four
Vectors in Special Relativity
There are many important quantities that transform like 4-Vectors. They are defined so that the "length" of a 4-vector is invariant under a coordinate transformation.
Space-Time 4-Vector; Length Contraction and Time
Dilatation
The space-time 4-Vector is defined by:
![]() or
or
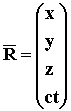 (9)
(9)
The length of the space-time 4-Vector squared is given by:
![]() (10)
(10)
In differential form,
![]() or space interval squared
or space interval squared
![]() is:
is:
![]() (11)
(11)
The Lorentz Transformation can be expressed in matrix form using the Lorentz matrix D:
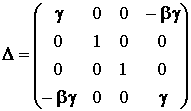 (12)
(12)
This acts on the 4-vector coordinates of a world point in S and gives their values in Sí:
 (13)
(13)
The matrices product gives relations (7).