Velocity
4-Vector
In Newtonian
mechanics, the velocity in x direction for example, is defined as
![]() so it might be thought that
so it might be thought that
![]() is the analogous quantity, where xi is a coordinate of
the space-time 4-Vector.
is the analogous quantity, where xi is a coordinate of
the space-time 4-Vector.
However, dt is not Lorentz invariant.
Instead, we should differentiate with respect to a Lorentz invariant quantity. Weíll use the proper time, dt, which is just time according to the frame of particle at its location.
![]() (14)
(14)
Where ds is the space-time interval.
Hence, the 4-velocity of a particle can be written as:
![]() (15)
(15)
where its components are:
![]() or
or
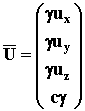 (16)
(16)
where ux, uy, uz, are the speed-components of a particle moving in the frame S.
If Lorentz matrix D
acts on the 4-Vector
![]() , we get the particle speed components
, we get the particle speed components
![]() in the Sí frame.
in the Sí frame.
 (16)
(16)
The matrices product gives:
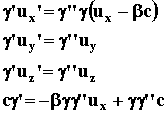 (17)
(17)
From the last expression, we obtain:
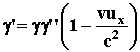 (18)
(18)
This one will be substitute in the first three relations, and we get:
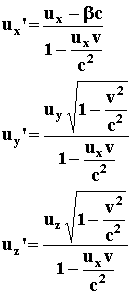 (19)
(19)
One can compute the particle total speed uí in the Sí frame:
![]() and we get the following
expression:
and we get the following
expression:
 (20)
(20)