If we divide the momentum-energy 4-vector by the
rationalized Planck constant (or Dirac constant)
![]() , we get the wave 4-Vector:
, we get the wave 4-Vector:
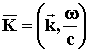 or
or
 (25)
(25)
where
![]() is the wave vector associated with
the wave number
is the wave vector associated with
the wave number
![]() . It is related to the momentum
. It is related to the momentum
![]() , by
, by
![]() . The energy can be expressed as
. The energy can be expressed as
![]() , where
, where
![]() .
.
The Lorentz transformation allows us to derive the wave frequency an observer sees according to the wave frequency emitted in the source frame.
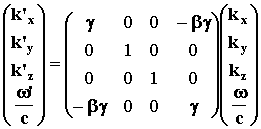 (26)
(26)
From the matrices product, we get:
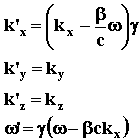 (27)
(27)
The last one is the most important of them, representing the Doppler effect, i.e., a change in the observer frequency of a wave as a result of relative motion between the source and the observer.
![]() can be written as
can be written as
![]() ,
,
Therefore:
 (28)
(28)
But,
![]() , so
, so
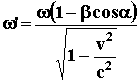 ; Because
; Because
![]() , we obtain:
, we obtain:
 (29)
(29)
If one consider the case in which the direction of the propagation of wave and the relative velocity of the S and Sí frame do coincide, we obtain longitudinal Doppler effect.
If the source travels strait away from the observer,
![]()
![]() and
and
 (30)
(30)
If the source travels toward the
observer,
![]() , so
, so
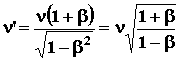 (31)
(31)
If an observer moving relative to the sourceís frame S, looks perpendicularly at the wave source which emits at the frequency n, he will measure a modified frequency.
Hence:
![]() , so
, so
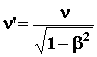 (32)
(32)