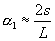
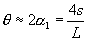
but for small q you find also the relation
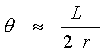
a) Outer radius of the vertex detector: 13 cm
b) The magnetic field comes out of the picture
c) Five particles are produced right after the interaction. One of them, the Ks, decays into two pions.
d) The Ks is neutral because it's trajectory is strait.
e) If the Ks escapes from the interaction point with the velocity of light it gets s = c*t = 2.68 cm, where t is the lifetime of the particle.
f) it actually gets about 17 cm. The lifetime of the particle is refered to the system in which the particle is at rest. In the detector system, the lifetime of the particle is longer due to time dilatation! Or from the point of Lorentz contraction: looking from a inertial system which moves with the Ks the distance of 17 cm looks like
g) l' = l / g g: gamma factor. For l = 2.68 cm and l' = 17 cm g = 6,34 ==> b = 0.918 c
h) The track in the picture is only a projection in the x-y-plane. The Ks has also a component in the z-direction. So the track of the Ks and therefore it' velocity is even bigger!
back to exercise 1 back to intro
Sagitta s = 1.0306 mm and L = 13.687 cm
back to exercise 2a back to intro
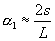
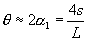
but for small q you find also the relation
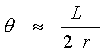
Combining the two relations gives the requested equation ![]()
back to exercise 2b back to intro
Solutions to exercise 2c: r = 227 cm
back to exercise 2c back to intro
centripetal force:
![]()
back to exercise 3a back to intro
Lorentz force:
![]()
back to Exercise 3b back to intro
q v B = p v/r => q B = p / r == > p = r q B
pt = 1,047 GeV/c
back to exercise 3c back to intro
pt / p = sin q => p = pt / sin q = 1,129 GeV/c
back to exercise 3d back to intro
| particle | K- | p- | p+ | p+ | p+ | p- |
| E (GeV) | 3.398 | 1.138 | 5.17 | 0.592 | 0.381 | 0.926 |
back to exercise 3e back to intro
The mass of the top quark is about 175 GeV, and is therefore much too big for a top-antitop pair to have been produced in a 200 GeV collision. The masses of all other quarks are all small enough. In particular, the mass of the bottom quark is about 4.4 GeV So the total of the energy of a bottom antibottom pair would be around 9 GeV. There is a fairly high probability, that a bottom-antibottom-state has been observed.
back to exercise 4 back to intro
a) A single muon cannot be produced on its own as charge and muon-lepton number must be conserved.
b)
![]()
The mass of the muon is very small compared to the total energy of the particle. p = 99.99994 GeV/c
c) Combining the formulas for the centripetal and the Lorentz force, you get an equation for the momentum p = r q B. You can calculate the radius r = p /qB = 222 m
d) In the tracking problem you derived the relation between the radius
of the track, the sagitta and L:
![]() . The
radial diameter of the time projection chamber has to be more than 3 meters!
. The
radial diameter of the time projection chamber has to be more than 3 meters!