
The goal of analyzing the data from an event is to calculate the masses, energies and the momenta of all the particles produced in the event. To calculate the momentum of a charged particle you have to know the radius of its track. In this exercise you will learn how to calculate this radius from only three equidistant points on the track.
If a charged particle passes through a detector, there will be several hits (signals) in the chamber along the track of the particle. In the event in the previous section, for example, you can see the hits (dots along the colored lines) of several particles. The electronics in the detector will produce a set of coordinates for these hits. In the time projection chamber for example, the particles have left about ten to twenty hits. Using sophisticated statistical methods, the physicists try to find the curve that best fits the coordinates of the hits. That means all the hits lie almost on this circle.

Consider three points P1, P2 and P3 which lie on a circle. To keep the calculation simple, suppose that point P2 lies in the middle plane between the two other points. To calculate the radius r of the trajectory you first have to calculate the sagitta s and L, which is the distance between the points P1 and P3. If you know the coordinates of the points it is easy to calculate s and L.
Calculate s and L forthe coordinates of the three points P1, P 2 and P 3, which are from the orange track. The center of the coordinate system lies on the beam axis.
| Track 2 | x (cm) | y (cm) |
| P1 | -148.327 | -29.9367 |
| P2 | -154.138 | -33.5045 |
| P3 | -159.885 | -37.2683 |
Click here for Solutions of Exercise 2a
Now, once you know s and L, you can calculate the radius r of the trajectory with a geometrical calculation using the following approximation:
If s << L ==> a1 is small and therefore
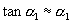
and q is small and therefore
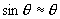
Using these approximations, show that the radius of the trajectory is
![]() .
.
Click here for Solutions of Exercise 2b
Calculate the r for the three points form above.
Click here for Solutions of Exercise 2c
Calculating the energy and momentum from the track radius