and energy E
concerns two particle systems where one can calculate each particle momentum and
energy in the center-of-mass frame of reference if their values in the
laboratory frame are known, as well as the particles’ rest masses.Applications of Special Relativity on Particle Physics
Most of what is known about particle physics comes from measuring what emerges from a collision of one particle with another in an instrument called detector, which is an instrument that can record the passage of particles through it.
The experimental side of this subject is based on BUBBLE CHAMBER DETECTOR in many laboratories around the world, such as CERN-Geneva and Fermilab. The great advantage of bubble chambers is their ability to pick up details of complicated interactions: by following the trails of bubbles one can see subsequent interactions and decays of the products of the initial interaction.
Two particle Collision in the Laboratory and Center of Mass Frame
An
interesting application of the transformation formula of momentum
and energy E
concerns two particle systems where one can calculate each particle momentum and
energy in the center-of-mass frame of reference if their values in the
laboratory frame are known, as well as the particles’ rest masses.
For
example, in a nuclear interaction, a nuclear projectile (nucleon, pion, kaon,
etc.) with the rest mass
and relativistic speed
collides a nuclear target with the
rest mass
.
The
total momentum of the two-particle system is
in the center-of-mass frame. It
moves with the c.m. velocity
with respect to the laboratory
frame.
Assuming
that
and
, we’ll get the
formula:
(2.1)
where:
(2.2)
(2.3)
are the total momentum and energy carried along by the two
particle system in the laboratory frame where
the target is at rest.
The relation between the energy and momentum is:
(2.4)
Plugging (2.2) and (2.3) into (2.1) gives:
(2.5)
The particles’ momenta in the c.m. frame,
and
, as well as their energies
and
will be calculated using the
Lorentz’s transformation matrix.
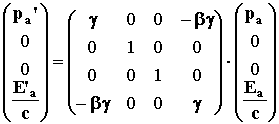(2.6)
respectively:
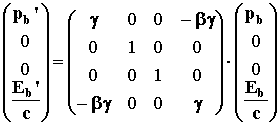(2.7)
where
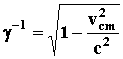and
These
formulae allow us to compute each particle momentum and energy in the c.m.
frame:
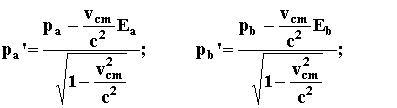(2.8)
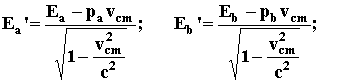(2.9)
Taking
into account that
and
in the laboratory frame, and
plugging (2.5) into (2.8)-(2.9), we get:
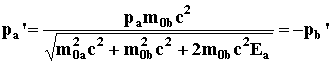(2.10)
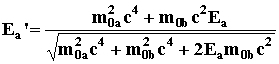(2.11)
(2.12
|
|
Let’s
consider a proton-neutron collision where
is the bombarding kinetic energy of
the proton projectile in the laboratory frame where the neutron rests.
The
particles’ rest energies are :
(proton) and
(neutron).
The
total energy of the proton projectile in the laboratory frame is:
. The c.m. velocity
with respect to the laboratory frame will be computed by formulae (2.4) and
(2.5), and the obtained value is
.
The
formulae (2.11) and (2.12) allow us to compute the particles’ energies in the
c.m. frame, which are very important for calculating interaction cross-sections,
collision times, etc. in different nuclear interactions. In this example, they
are:
(proton)
and
(neutron)
content
