
Bubble chambers have played an important role in experimental particle physics, yielding images that can be beautiful as well as informative.

Fig.1 The 3.7 m European bubble chamber BEBC (CERN, 1973): iron magnetic shielding ; lower and upper parts of the vacuum enclosure of the magnet; turbo-molecular vacuum pumps for the "fish-eye" windows; the two superconducting coils; a handling platform; the two cryostats suspended from the bar of the traveling crane which has a 170 ton carrying capacity. The chamber proper, not dismantled, is inside the shielding.
Aim:
To get as close as possible to measure energy E and momentum
![]() of all particles taking part in the interactions.
of all particles taking part in the interactions.
Steps:
Find all events and classify them. Individual particle tracks have several characteristics that can be used to identify their properties.
Track length: this is related to the particle energy, but also depends on the type of the particles. This feature is very useful when the particles stops (almost always for protons).
Track thickness: this is related to charge and particle speed. Highly charged particles tend to produce thicker tracks. Faster particles produce thinner tracks.
Track curvature: If the direction is which the particle are traveling is known, then the sign of their charge can be worked out from the direction in which they are deflected. As particles move through a medium, they lose energy which mean that the radius of curvature of their path becomes smaller, and they spiral. If this is visible in the track, the direction of motion can be deduced.
·
Measuring
1. The coordinates of several points on each track are measured on three bubble chamber views. From these, a computer program calculates the best curvatures fitting the measurements of the tracks and hence their momenta.
1.
A charged particle traveling through a magnetic field
![]() with a speed
with a speed
![]() experience a Lorentz force
experience a Lorentz force
![]() . If the motion is perpendicular to the field, particles follows a circular path
of radius r, and the motion is described by :
. If the motion is perpendicular to the field, particles follows a circular path
of radius r, and the motion is described by :
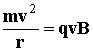 . From the radius of curvature, we get the particle momentum:
. From the radius of curvature, we get the particle momentum:
![]() . This relation is valid, whether the particle is relativistic or not.
. This relation is valid, whether the particle is relativistic or not.
2.
The momenta are given in terms of the three variables
![]() , where azimuthal angle
, where azimuthal angle
![]() are measured clockwise in the plan of the picture from
an arbitrary axis going roughly in the direction of the incident beam;
dip angle
are measured clockwise in the plan of the picture from
an arbitrary axis going roughly in the direction of the incident beam;
dip angle
![]() are the angles the tracks made with
the plan of the picture.
are the angles the tracks made with
the plan of the picture.
3. Missing tracks: Sometimes certain events in the bubble chamber are connected even though no visible track connects them. This is a good indication that a neutral particle is involved in the reaction.
The laws of conservation of energy, momentum and charge can help to identify unknown particles from the behavior of familiar ones.
![]() applications of special relativity
applications of special relativity